Research

Fast and memory-efficient algorithms are essential for working with larger and larger amounts of data. Theoretical computer scientists concern themselves with designing these algorithms, and proving important properties such as their correctness, their running time and their space usage. So far, my research has mostly been on the design of algorithms on graphs and strings.

The main real-world application of string algorithms is in bioinformatics, for the analysis of large amounts of DNA. For example, a common task in bioinformatics is sequence alignment, where the genomes of two or more species are put together to identify sections that they have in common and sections where they are different. Because these DNA sequences can be very long (a human genome is longer than 3 billion base pairs!), efficient string algorithms are needed to perform these analyses.

Sampling techniques for faster string algorithms

In 2024, I co-authored two papers related to string sampling mechanisms. Sampling is an important technique in string algorithm, that reduces the whole string to a small set of representative positions, that for the purpose of an algorithm still conveys the same information as the whole string.

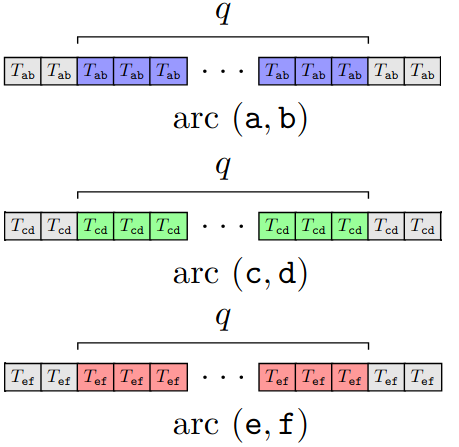
One sampling mechanism is called “minimizers”, and involves selecting small fragments of the string that are lexicographically smaller than their surrounding fragments. In Minimizing the Minimizers through Alphabet Reordering, we studied the effect of different alphabet orders on the number of minimizers in a string. It turns out that the number of minimizers can be significantly smaller under one ordering than another, which can greatly impact the running time of algorithms using minimizers. A natural question is thus: can we find the optimal alphabet order, that minimizes the number of minimizers for a given string? Our main result is that this problem is NP-hard through a reduction from Feedback Arc Set, which means that it would most likely take an exponential amount of time to find the optimal ordering for any given string. However, it remains an open question if this is also true for general (non-lexicographic) orders, or other specific classes.

In Sparse Suffix and LCP Array: Simple, Direct, Small and Fast, we studied the sparse suffix array (SSA), a common string data structure that is often used in tandem with sampling mechanisms. The sparse suffix array takes, for a sample of positions in a string, all suffixes starting at these positions and sorts them lexicographically. It is usually combined with the LCP (longest common prefix) array, which tells us the longest prefix that two consecutive entries of the SSA have in common. Together, they allow us to quickly find occurrences of patterns starting at any of the sampled positions.

There exist many algorithms for constructing the SSA of a string, but most have the drawback of consuming a very large amount of space, proportional to the size of the input string. Moreover, they tend to be quite complicated and therefore difficult to implement. We developed an algorithm that could be implemented quite easily, and uses very little space on top of the memory needed to store the input string (its additional space usage is proportional to the size of the sample). Moreover, this algorithm works especially fast if most of the values in the LCP array are quite short, which tends to be the case in practice. If the number of short LCP values is large enough, the running time is linear in the length of the input string.

Heavy nodes in a small neighborhood for money laundering detection

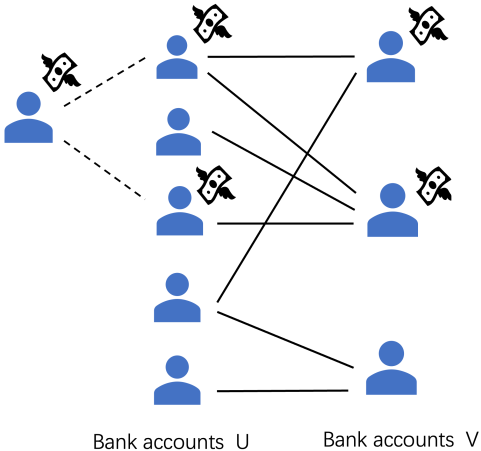
In the paper Heavy Nodes in a Small Neighborhood, we introduced the following graph problem. Given a bipartite graph $G$, with node sets $U$ and $V$, and a weight function for the nodes in $V$, we wish to find the subset of $V$ with the largest ratio between its total weight and number of neighbors.

The problem’s main motivation is the application of money laundering detection. When a large amount of money is laundered, it is generally divided between several accounts to eventually be transferred to the intended destination. Representing bank transfers in a graph structure, such suspicious activity expresses itself in heavy nodes (representing large amounts of money in accounts) with a small neighborhood (the accounts the money is transferred from). Nodes with less weight (like most people’s bank accounts) or heavy weight but many neighbors (like businesses with a lot of customers) will be seen as less suspicious. Therefore, algorithms for this problem can prove useful for actually detecting suspicious banking activity.

In our paper, we designed an exact algorithm that solves the problem in polynomial time using linear programming, and a number of approximation algorithms. The algorithms were implemented and tested on both real-world anonymized bank transactions as well as synthetic data, showing that they produce very accurate results with a fast running time.